|
|

Line drawing is our first adventure into the area of scan
conversion. The need for scan conversion, or rasterization, techniques is a
direct result of scanning nature of raster displays (thus the names).
Vector displays are particularly well suited for the display of lines. All that
is needed on a vector display to generate a line is to supply the appropriate
control voltages to the x and y deflection circuitry, and the electron beam
would traverse the line illuminating the desired segment. The only inaccuracies
in the lines drawn a vector display resulted from various non-linearities, such
as quantization and amplifier saturation, and the various noise sources in the
display circuitry.
When raster displays came along the process of drawing lines became more difficult.
Luckily, raster display pioneers could benefit from previous work done in the
area of digital plotter algorithms. A pen-plotter is a hardcopy device used
primarily to display engineering line drawings. Digital plotters, like raster
displays, are discretely addressable devices, where position of the pen on a
plotter is controlled by special motors called stepper motors that are connected
to mechanical linkages that translates the motor's rotation into a linear translation.
Stepper motors can precisely turn a fraction of a rotation (for example 2 degrees)
when the proper controlling voltages are applied. A typical flat-bed plotter
uses two of these motors, one for the x-axis and a second for the y-axis, to
control the position of a pen over a sheet of paper. A solenoid is used to raise
and lower the actual pen when drawing and positioning.
The bottom line is that most of the popular line-drawing algorithms used to
on computer screens (and laser and ink-jet printers for that matter) were originally
developed for use on pen-plotters. Furthermore, most of this work is attributed
by a single man, Jack Bresenham, who was an IBM employee. He is currently a
professor at Winthrop University.
In this lecture we will gradually evolve from the basics of algebra to the famous
Bresenham line-drawing algorithms (along the same lines as a famous paper by
Bob Sproull), and then we will discuss some developments that have happened
since then.
CRTs were embraced as output devices very early in the development of digital computers.
There close cousins, vacuum tubes, were some of the first
switching elements used to build computers. Today, the CRT is a the last remaining
vacuum tube in most systems (Even the flashing lights are solid-state LEDs).
Most likely, oscilloscopes were some of the first computer graphics displays.
The results of computations could be used to directly drive the vertical and
horizontal displacement plates in order to draw lines on the CRT's face. By
varying the current to the heating filament the output of the electron beam
could also be controlled. This allowed the intensity of the lines to vary from
bright to completely dark.
These early CRT displays were called vector, calligraphic or affectionately
stroker displays. The demonstration above gives some feel for how they worked.
By the way, this demo is an active Java applet. You can click and drag your
mouse inside of the image to reorient the CRT for a better view. Notice the
wireframe nature of the displayed image. This demo is complicated by the fact
that it's a wireframe simulation of a wireframe display system. Notice how the
color of the gray lines of the CRT vary from dark to light indicating which
parts of the model that are closer to the viewer. This technique is called depth-cueing,
and it was used frequently on vector displays.
The intensity variations seen on the teapot, however, are for a different reason.
Eventually, the phosphors recover from their excited state and the displaced
electrons return back to their original bands. The glow of the phosphor fades.
Thus, the image on the CRT's face must be constantly redrawn, refreshed, or
updated. The two primary problems with vector displays are that they required
constant updates to avoid fading, thus limiting the drawn scene's complexity,
and they only drew wireframes.

Line drawing is our first adventure into the area of scan
conversion. The need for scan conversion, or rasterization, techniques is a
direct result of scanning nature of raster displays (thus the names).
Vector displays are particularly well suited for the display of lines. All that
is needed on a vector display to generate a line is to supply the appropriate
control voltages to the x and y deflection circuitry, and the electron beam
would traverse the line illuminating the desired segment. The only inaccuracies
in the lines drawn a vector display resulted from various non-linearities, such
as quantization and amplifier saturation, and the various noise sources in the
display circuitry.
When raster displays came along the process of drawing lines became more difficult.
Luckily, raster display pioneers could benefit from previous work done in the
area of digital plotter algorithms. A pen-plotter is a hardcopy device used
primarily to display engineering line drawings. Digital plotters, like raster
displays, are discretely addressable devices, where position of the pen on a
plotter is controlled by special motors called stepper motors that are connected
to mechanical linkages that translates the motor's rotation into a linear translation.
Stepper motors can precisely turn a fraction of a rotation (for example 2 degrees)
when the proper controlling voltages are applied. A typical flat-bed plotter
uses two of these motors, one for the x-axis and a second for the y-axis, to
control the position of a pen over a sheet of paper. A solenoid is used to raise
and lower the actual pen when drawing and positioning.
The bottom line is that most of the popular line-drawing algorithms used to
on computer screens (and laser and ink-jet printers for that matter) were originally
developed for use on pen-plotters. Furthermore, most of this work is attributed
by a single man, Jack Bresenham, who was an IBM employee. He is currently a
professor at Winthrop University.
In this lecture we will gradually evolve from the basics of algebra to the famous
Bresenham line-drawing algorithms (along the same lines as a famous paper by
Bob Sproull), and then we will discuss some developments that have happened
since then.
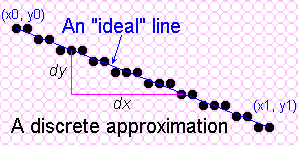
Note that since vector-graphics displays, capable of drawing nearly perfect
lines, predated raster-graphics displays. Thus, the expectations for line quality
were set very high. The nature of raster-graphics display, however, only allows
us to display a discrete approximation of a line, since we are restricted to
only turn on discrete points, or pixels. In order to discuss, line drawing we
must first consider the mathematically ideal line (or line segment).
From geometry we know that a line, or line segment, can be uniquely specified
by two points. From algebra we also know that a line can be specified by a slope,
usually given the name m and a y-axis intercept called b. Generally in computer
graphics, a line will be specified by two endpoints. But the slope and y-intercept
are often calculated as intermediate results for use by most line-drawing algorithms.
The goal of any line drawing algorithm is to construct the best possible approximation
of an ideal line given the inherent limitations of a raster display.
Based on the simple slope-intercept algorithm from algebray = m x + by0 = m x0 + by1 = m x1 + bm = (y1 - y0)/(x1 - x0) = dy/dxb = y0 - m x0 |
public void lineSimple(int x0, int y0, int x1, int y1, Color color) {
int pix = color.getRGB();
int dx = x1 - x0;
int dy = y1 - y0;
raster.setPixel(pix, x0, y0);
if (dx != 0) {
float m = (float) dy / (float) dx;
float b = y0 - m*x0;
dx = (x1 > x0) ? 1 : -1;
while (x0 != x1) {
x0 += dx;
y0 = Math.round(m*x0 + b);
raster.setPixel(pix, x0, y0);
}
}
}
|
The first line-drawing algorithm presented is called the simple slope-intercept algorithm. It is a straight forward implementation of the slope-intercept formula for a line.
 |
Problem: lineSimple( ) does not give satisfactory results for slopes > 1Solution: symmetry
public void lineImproved(int x0, int y0, int x1, int y1, Color color) {
int pix = color.getRGB();
int dx = x1 - x0;
int dy = y1 - y0;
raster.setPixel(pix, x0, y0);
if (Math.abs(dx) > Math.abs(dy)) { // slope < 1
float m = (float) dy / (float) dx; // compute slope
float b = y0 - m*x0;
dx = (dx < 0) ? -1 : 1;
while (x0 != x1) {
x0 += dx;
raster.setPixel(pix, x0, Math.round(m*x0 + b));
}
} else if (dy != 0) { // slope >= 1
float m = (float) dx / (float) dy; // compute slope
float b = x0 - m*y0;
dy = (dy < 0) ? -1 : 1;
while (y0 != y1) {
y0 += dy;
raster.setPixel(pix, Math.round(m*y0 + b), y0);
}
}
}
|
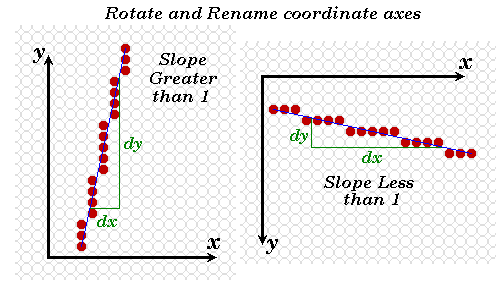
It doesn't make sense to begin optimizing an algorithm before satisfies its
design requirements! Code is usually developed under considerable time pressures.
If you start optimizing before you have a working prototype you have no fall
back position.
Our simple line drawing algorithm does not provide satisfactory results for
line slopes greater than 1.
The solution: symmetry.

The assigning of one coordinate axis the name x and the other y was an arbitrary choice. Notice that line slopes of greater than one under one assignment result in slopes less than one when the names are reversed. We can modify the lineSimple( ) routine to exploit this symmetry as shown above.
Optimize those code fragments where the algorithm spends most of its
time.
|
|
The most important code fragments to consider when
optimizing are those where the algorithm spends most of its time. Often these
areas are within loops.
Our improved algorithm can be partitioned into two major sections. The first
section is basically set-up code that is used by the second section, the central
pixel-drawing while-loop. Most of the pixels are drawn in this while loop.
First optimization: remove unnecessary method invocations. Notice the call to the round class-method of the Math object that is executed for each pixel drawn. You might think that proper rounding is so trival a task that it hardly warrants a special method to begin with. But, it is complicated when differences between postive and negative numbers, and proper handling of fractions with a value of exactly 0.5 are considered.
However, in our line drawing code we are either not going to run into these cases (i.e. we only consider positive coordinate values) or we don't care (i.e. we don't expect to see values of 0.5 very often, and when we do we'd like to see them handled consistently). So for our purposes the call to Math.round(m*x0 + b) could be replaced with the following (int)(m*x0 + b + 0.5).
Second optimization: use incremental calculations.
Incremental or iterative function calculations use previous function values to compute future values. Often expressions within loops depend on a value that is being incremented or decremented on each loop iteration. In these cases the actual function values might be more efficiently calculated by first computing an initial value of the function during the loop set up, and updating the subsequent function values using a discrete version of a differential equation called a difference equation.
Consider the expression,
m*x0 + b + 0.5,
that is computed inside the first loop. The We can initialize the first value
of the function outside of the loop:
y[0] = m*x0 + b + 0.5
. Future values of y depend only on how the value of x changes within the loop,
since all other values are constant. Thus subsequent values of y can be computed
by one of the following equations:
y[i+1] = y[i] + m; // if x0 is incremented
or
y[i+1] = y[i] - m; // if x0 is decremented
We can use a single equation if we change the sign of m, based on whether we
are incrementing or decrementing, outside of the loop.
Last optimisation : use of integer operation instead of float one.
public void lineDDA(int x0, int y0, int x1, int y1, Color color) {
int pix = color.getRGB();
int dy = y1 - y0;
int dx = x1 - x0;
float t = (float) 0.5; // offset for rounding
raster.setPixel(pix, x0, y0);
if (Math.abs(dx) > Math.abs(dy)) { // slope < 1
float m = (float) dy / (float) dx; // compute slope
t += y0;
dx = (dx < 0) ? -1 : 1;
m *= dx;
while (x0 != x1) {
x0 += dx; // step to next x value
t += m; // add slope to y value
raster.setPixel(pix, x0, (int) t);
}
} else { // slope >= 1
float m = (float) dx / (float) dy; // compute slope
t += x0;
dy = (dy < 0) ? -1 : 1;
m *= dy;
while (y0 != y1) {
y0 += dy; // step to next y value
t += m; // add slope to x value
raster.setPixel(pix, (int) t, y0);
}
}
}
Incorporating these changes into our previous lineImproved( ) algorithm gives the following result
Low-Level Optimizations
Low-level optimizations are somewhat dubious, because they depend on understanding
various machine details. Because machines vary, the accuracy of these low-level
assumptions can sometimes be questioned.
Typically, a set of general rules can be determined that are more-or-less consistent
across machines. Here are some examples:
* Addition and Subtraction are generally faster than Multiplication.
* Multiplication is generally faster than Division.
* Using tables to evaluate discrete functions is faster than computing them
* Integer caluculations are faster than floating-point calculations.
* Avoid unnecessary computation by testing for various special cases.
* The intrinsic tests available to most machines are greater than, less than,
greater than or equal, and less than or equal to zero (not an arbitrary value).
None of these rules are etched in stone. Some of these rules are becoming
less and less valid as time passes. We'll address these issues in more detail
later.
For our line drawing algorithm we'll investigate applying several of these optimizations. The incremental calculation effectively removed multiplications in favor of additions. Our next optimization will use three of the mentioned methods. It will remove floating-point calculations in favor of integer operations, and it will remove the single divide operation (it makes a difference on short lines), and it will normalize the tests to tests for zero.
m = (y1 - y0) / (x1 - x0)
yi+1 = yi + m
fraction += m;
if (fraction >= 1) {
y = y + 1; fraction -= 1;
}
Notice that the slope is always rational (a ratio
of two integers).
Also note that the incremental part of the algorthim
never generates a new y value that is more than one unit away from the old one,
because the slope is always less than one (this assured by our improved algorithm).
fraction = 1/2 + dy/dx
scaledFraction = dx + 2*dy
scaledFraction += 2*dy // 2*dx*(dy/dx)
if (scaledFraction >= 2*dx) { ... }
OffsetScaledFraction = dx + 2*dy - 2*dx = 2*dy - dx,
OffsetScaledFraction += 2*dy
if (OffsetScaledFraction >= 0) {
y = y +1; OffsetScaledFraction -= 2*dx;
}
public void lineBresenham(int x0, int y0, int x1, int y1, Color color) {
int pix = color.getRGB();
int dy = y1 - y0;
int dx = x1 - x0;
int stepx, stepy;
if (dy < 0) { dy = -dy; stepy = -1;
} else { stepy = 1;
}
if (dx < 0) { dx = -dx; stepx = -1;
} else { stepx = 1;
}
dy <<= 1; // dy is now 2*dy
dx <<= 1; // dx is now 2*dx
raster.setPixel(pix, x0, y0);
if (dx > dy) {
int fraction = dy - (dx >> 1); // same as 2*dy - dx
while (x0 != x1) {
if (fraction >= 0) {
y0 += stepy;
fraction -= dx; // same as fraction -= 2*dx
}
x0 += stepx;
fraction += dy; // same as fraction -= 2*dy
raster.setPixel(pix, x0, y0);
}
} else {
int fraction = dx - (dy >> 1);
while (y0 != y1) {
if (fraction >= 0) {
x0 += stepx;
fraction -= dy;
}
y0 += stepy;
fraction += dx;
raster.setPixel(pix, x0, y0);
}
}
}
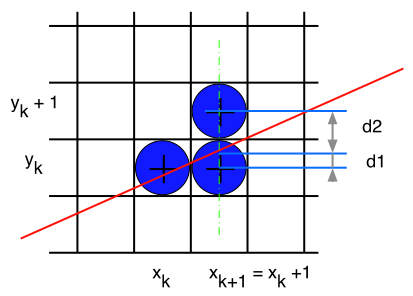
recursive process
y = m (xk + 1) + bd1 = y - yk = m (xk + 1) + b - ykd2 = (yk + 1) - y = yk + 1 - m (xk + 1) -bwhat we want to know : which of d1 and d2 is smaller, what we'll study : the sign of d1 - d2d1 - d2 = 2 m (xk + 1) - 2 yk + 2b -1 |
 |
public void lineBresenham(int x0, int y0, int x1, int y1, Color color) {
int pix = color.getRGB();
int dy = y1 - y0;
int dx = x1 - x0;
int stepx, stepy;
if (dy < 0) { dy = -dy; stepy = -1;
} else { stepy = 1;
}
if (dx < 0) { dx = -dx; stepx = -1;
} else { stepx = 1;
}
dy <<= 1; // dy is now 2*dy
dx <<= 1; // dx is now 2*dx
raster.setPixel(pix, x0, y0);
if (dx > dy) {
int fraction = dy - (dx >> 1); // same as 2*dy - dx
while (x0 != x1) {
if (fraction >= 0) {
y0 += stepy;
fraction -= dx; // same as fraction -= 2*dx
}
x0 += stepx;
fraction += dy; // same as fraction -= 2*dy
raster.setPixel(pix, x0, y0);
} } else { ... }
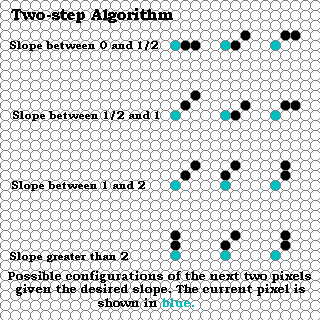
Most books would have you believe that the development of line drawing algorithms
ended with Bresenham's famous algorithm. But there has been some signifcant
work since then.
The two-step algorithm takes the interesting approach of treating line drawing as a automaton, or finite state machine. If one looks at the possible configurations that the next two pixels of a line, it is easy to see that only a finite set of possiblities exist.
The two-step algorithm also exploits the symmetry of line-drawing by simultaneously drawn from both ends towards the midpoint.
The code, which is further down this web page, is a bit long to show an a slide.
public void lineTwoStep(int x0, int y0, int x1, int y1, Color color) {
int pix = color.getRGB();
int dy = y1 - y0;
int dx = x1 - x0;
int stepx, stepy;
if (dy < 0) { dy = -dy; stepy = -1; } else { stepy = 1; }
if (dx < 0) { dx = -dx; stepx = -1; } else { stepx = 1; }
raster.setPixel(pix, x0, y0);
raster.setPixel(pix, x1, y1);
if (dx > dy) {
int length = (dx - 1) >> 2;
int extras = (dx - 1) & 3;
int incr2 = (dy << 2) - (dx << 1);
if (incr2 < 0) {
int c = dy << 1;
int incr1 = c << 1;
int d = incr1 - dx;
for (int i = 0; i < length; i++) {
x0 += stepx;
x1 -= stepx;
if (d < 0) { // Pattern:
raster.setPixel(pix, x0, y0); //
raster.setPixel(pix, x0 += stepx, y0); // x o o
raster.setPixel(pix, x1, y1); //
raster.setPixel(pix, x1 -= stepx, y1);
d += incr1;
} else {
if (d < c) { // Pattern:
raster.setPixel(pix, x0, y0); // o
raster.setPixel(pix, x0 += stepx, y0 += stepy); // x o
raster.setPixel(pix, x1, y1); //
raster.setPixel(pix, x1 -= stepx, y1 -= stepy);
} else {
raster.setPixel(pix, x0, y0 += stepy); // Pattern:
raster.setPixel(pix, x0 += stepx, y0); // o o
raster.setPixel(pix, x1, y1 -= stepy); // x
raster.setPixel(pix, x1 -= stepx, y1); //
}
d += incr2;
}
}
if (extras > 0) {
if (d < 0) {
raster.setPixel(pix, x0 += stepx, y0);
if (extras > 1) raster.setPixel(pix, x0 += stepx, y0);
if (extras > 2) raster.setPixel(pix, x1 -= stepx, y1);
} else
if (d < c) {
raster.setPixel(pix, x0 += stepx, y0);
if (extras > 1) raster.setPixel(pix, x0 += stepx, y0 += stepy);
if (extras > 2) raster.setPixel(pix, x1 -= stepx, y1);
} else {
raster.setPixel(pix, x0 += stepx, y0 += stepy);
if (extras > 1) raster.setPixel(pix, x0 += stepx, y0);
if (extras > 2) raster.setPixel(pix, x1 -= stepx, y1 -= stepy);
}
}
} else {
int c = (dy - dx) << 1;
int incr1 = c << 1;
int d = incr1 + dx;
for (int i = 0; i < length; i++) {
x0 += stepx;
x1 -= stepx;
if (d > 0) {
raster.setPixel(pix, x0, y0 += stepy); // Pattern:
raster.setPixel(pix, x0 += stepx, y0 += stepy); // o
raster.setPixel(pix, x1, y1 -= stepy); // o
raster.setPixel(pix, x1 -= stepx, y1 -= stepy); // x
d += incr1;
} else {
if (d < c) {
raster.setPixel(pix, x0, y0); // Pattern:
raster.setPixel(pix, x0 += stepx, y0 += stepy); // o
raster.setPixel(pix, x1, y1); // x o
raster.setPixel(pix, x1 -= stepx, y1 -= stepy); //
} else {
raster.setPixel(pix, x0, y0 += stepy); // Pattern:
raster.setPixel(pix, x0 += stepx, y0); // o o
raster.setPixel(pix, x1, y1 -= stepy); // x
raster.setPixel(pix, x1 -= stepx, y1); //
}
d += incr2;
}
}
if (extras > 0) {
if (d > 0) {
raster.setPixel(pix, x0 += stepx, y0 += stepy);
if (extras > 1) raster.setPixel(pix, x0 += stepx, y0 += stepy);
if (extras > 2) raster.setPixel(pix, x1 -= stepx, y1 -= stepy);
} else
if (d < c) {
raster.setPixel(pix, x0 += stepx, y0);
if (extras > 1) raster.setPixel(pix, x0 += stepx, y0 += stepy);
if (extras > 2) raster.setPixel(pix, x1 -= stepx, y1);
} else {
raster.setPixel(pix, x0 += stepx, y0 += stepy);
if (extras > 1) raster.setPixel(pix, x0 += stepx, y0);
if (extras > 2) {
if (d > c)
raster.setPixel(pix, x1 -= stepx, y1 -= stepy);
else
raster.setPixel(pix, x1 -= stepx, y1);
}
}
}
}
} else {
int length = (dy - 1) >> 2;
int extras = (dy - 1) & 3;
int incr2 = (dx << 2) - (dy << 1);
if (incr2 < 0) {
int c = dx << 1;
int incr1 = c << 1;
int d = incr1 - dy;
for (int i = 0; i < length; i++) {
y0 += stepy;
y1 -= stepy;
if (d < 0) {
raster.setPixel(pix, x0, y0);
raster.setPixel(pix, x0, y0 += stepy);
raster.setPixel(pix, x1, y1);
raster.setPixel(pix, x1, y1 -= stepy);
d += incr1;
} else {
if (d < c) {
raster.setPixel(pix, x0, y0);
raster.setPixel(pix, x0 += stepx, y0 += stepy);
raster.setPixel(pix, x1, y1);
raster.setPixel(pix, x1 -= stepx, y1 -= stepy);
} else {
raster.setPixel(pix, x0 += stepx, y0);
raster.setPixel(pix, x0, y0 += stepy);
raster.setPixel(pix, x1 -= stepx, y1);
raster.setPixel(pix, x1, y1 -= stepy);
}
d += incr2;
}
}
if (extras > 0) {
if (d < 0) {
raster.setPixel(pix, x0, y0 += stepy);
if (extras > 1) raster.setPixel(pix, x0, y0 += stepy);
if (extras > 2) raster.setPixel(pix, x1, y1 -= stepy);
} else
if (d < c) {
raster.setPixel(pix, stepx, y0 += stepy);
if (extras > 1) raster.setPixel(pix, x0 += stepx, y0 += stepy);
if (extras > 2) raster.setPixel(pix, x1, y1 -= stepy);
} else {
raster.setPixel(pix, x0 += stepx, y0 += stepy);
if (extras > 1) raster.setPixel(pix, x0, y0 += stepy);
if (extras > 2) raster.setPixel(pix, x1 -= stepx, y1 -= stepy);
}
}
} else {
int c = (dx - dy) << 1;
int incr1 = c << 1;
int d = incr1 + dy;
for (int i = 0; i < length; i++) {
y0 += stepy;
y1 -= stepy;
if (d > 0) {
raster.setPixel(pix, x0 += stepx, y0);
raster.setPixel(pix, x0 += stepx, y0 += stepy);
raster.setPixel(pix, x1 -= stepy, y1);
raster.setPixel(pix, x1 -= stepx, y1 -= stepy);
d += incr1;
} else {
if (d < c) {
raster.setPixel(pix, x0, y0);
raster.setPixel(pix, x0 += stepx, y0 += stepy);
raster.setPixel(pix, x1, y1);
raster.setPixel(pix, x1 -= stepx, y1 -= stepy);
} else {
raster.setPixel(pix, x0 += stepx, y0);
raster.setPixel(pix, x0, y0 += stepy);
raster.setPixel(pix, x1 -= stepx, y1);
raster.setPixel(pix, x1, y1 -= stepy);
}
d += incr2;
}
}
if (extras > 0) {
if (d > 0) {
raster.setPixel(pix, x0 += stepx, y0 += stepy);
if (extras > 1) raster.setPixel(pix, x0 += stepx, y0 += stepy);
if (extras > 2) raster.setPixel(pix, x1 -= stepx, y1 -= stepy);
} else
if (d < c) {
raster.setPixel(pix, x0, y0 += stepy);
if (extras > 1) raster.setPixel(pix, x0 += stepx, y0 += stepy);
if (extras > 2) raster.setPixel(pix, x1, y1 -= stepy);
} else {
raster.setPixel(pix, x0 += stepx, y0 += stepy);
if (extras > 1) raster.setPixel(pix, x0, y0 += stepy);
if (extras > 2) {
if (d > c)
raster.setPixel(pix, x1 -= stepx, y1 -= stepy);
else
raster.setPixel(pix, x1, y1 -= stepy);
}
}
}
}
}
}