Intersection between two circles (3)

Given O1(x1,y1,z1), O2(x2,y2,z2), the center of the circles and r1 and r2, their Radius

Given M(x,y,z) the intersection, then another way is ...

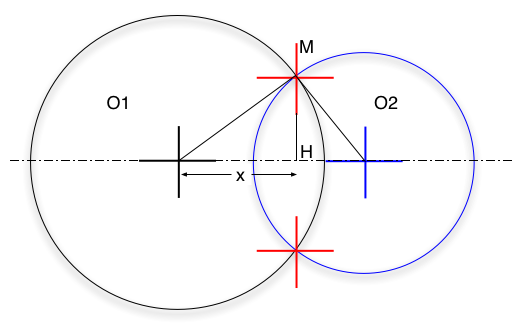O1H = x

MH = h

0102 = d

H02 = d - x

(1) R12 = h2 + x2

(2) R22 = h2 + (d - x )2 = h2 + d2 -2dx + x2

(2) - (1) R22 - R12 = d2 - 2dx

 

=> x = (d2 - R22 + R12)/2d

(1) h = +/- squareroot(R12 - x2)

M = O1 + O1 H +/- HM

Then O1H = x. O1O2/||O1O2||      then inverse -x and y of  O1O2/||O1O2|| vector to get an orthogonal vector