Locus of point defined by a constant view angle from 2 fixed points

Set of point defined by the fact that they form a given angle with two fixed points (A et B, of the Euclidian Plane).

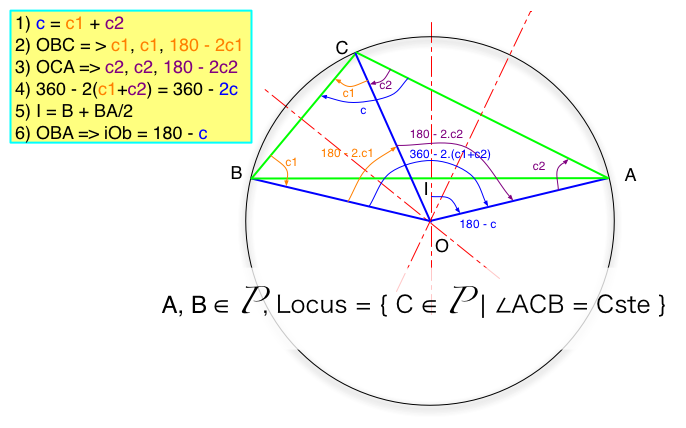
0) Given A, B and an angle c defined between 0 and 180°, positive from A to B. We will demonstrate that the set of point C such as aCb = c is indeed the arc AB (which arc AB is defined by the relative value of the angle compared to 90°). To achieve that, we consider one given C point that verify aCb = c and we look at the centre of the circum(scribed )circle for the triangle (ABC). We will indeed show that this circle can be describe without referring to C, but just AB and the angle c, and that therefore the possible set of C points are all on that circle.

1) Given ABC, it is well known that the circumscribed circle has its circumcenter O at the intersection of the 3 perpendicular bisectors of the triangle. Let's consider the two triangles (OCB) and (OAC) which share the common edge [OC]. c = c1 + c2

2) In all triangles, the somme of the angles equal to180. As O is on the perpendicular bisector of [CB], then (OCB) is a isosceles and therefore oCb = cBo = c1. From those two fact the last angle bOc = 180 - 2.c1

3) Likewise, in the isosceles triangle (OAC), we get cOa = 180 - 2.c2

4) bOa = bOc + cOa = 180 - 2.c1 + 180 - 2.c2 = 360 - 2 c

5) I is the middle of [AB], and then on its same perpendicular bisector as O. Therefore (IOB) is rectangle in I. Knowing I, A and the angle iOa = bOa / 2 = 180 - c, it is possible to defined O, without any reference to C. We have indeed demonstrate that given two fixed point A and B and an oriented angle c, the set of point C such as aCb = c is on the circle defined by its centre O and its radius OA.

NB. : Just note the effect of the orientation of the angle and its value relative to 90° to the selection of the part of the circle and the position of O relative to [AB]

links :

• Perpendicular Bisector : http://mathworld.wolfram.com/PerpendicularBisector.html
• Circumcircle : http://mathworld.wolfram.com/Circumcircle.html
  "The circumcircle is a triangle's circumscribed circle, i.e., the unique circle that passes through each of the triangles three vertices. The centre O of the circumcircle is called the circumcenter , and the circle's radius R is called the circumradius . A triangle's three perpendicular bisectors ,, and meet (Casey 1888, p. 9) at O(Durell 1928)."

PS. Question : why is the intersection of the 3 orthogonal bisectors the centre of the circumcircle ... ?