eScience Lectures Notes : Revisal of some basic Maths
Slide 1 : eScience : CG : Mathematics
Mathematics for Computer Graphics
Ref : Computer Graphics / Foley - VanDam - Feiner - Hughes
This part is somewhat theoritical, but it should not be
too difficult with a simple mathematical background
Slide 2 : Vector Space
Vector Space
Set of elements called vector, with 2 operations with certain properties:
usually we will note a vector in boldfaced letters or
with an arrows above it
1 ) Addition of vectors : commutative, associative, with an identity element
and each element must have inverses
- u + v = v + u
- u + ( v + w ) = (u + v
) + w
- there is 0 such as for any vector v, 0
+ v = v
- for every vector v, there is another vector w
such as v + w = 0 . w is written " -v
"
2 ) Scalar Multiplication : associative and distributive
- (ab)v = a (bv)
- 1v = v
- (a + b)v = av + bv
- a(v + w) =av + aw
Given those two operation, me may define a "linear combination"
of a set of vector v1, ... vn : any vector of the form
a1v1 + a2v2 + ... anvn
Example of Vector Space : Rn (the set of all ordered n-tuples of real number)
is a vector space
Sub example : R3 :
/ r1 / 1 / 4 / 5
| r2 ...... ex : | 3 + | 5 = |12
\ r3 \ 6 \ 2 \ 8
Slide 3 : Plane Vector Splace
One particular Vector Space : The Plane
We chose an origin, and every point of the plane is matched with the vector
that links the point to the chosen origin
We may then easily define...
The addition of two vector (the parallelogram rule)
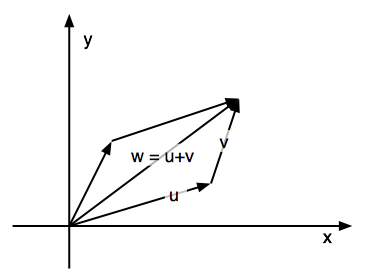
|
The multiplication of a vector by a scalar
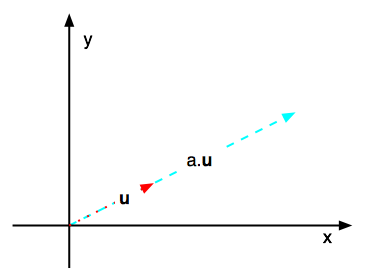
|
The vector 0 : the one which is matched with the chosen origin
Slide 4 : Affine Space
Affine Space
A set in which geometric operations make sense, but in which there is no distinguished
point
(i.e. no origin such as in a vector space)
A affine space consists of a set, called the points of the affine space, an
associated vector space and two operations which connect the affine and the
vector space
Given 2 Point P and Q, we can form the difference of P and Q which lies in
the vector Space
P - Q = v
Given a point P and a vector u, we can add u to P and get another point in
the affine space
P = Q + v
Properties to satisfy
(P + v) + u = P + (v + u)
P + u = P if and only if u = 0
Affine combination of the points P and Q by the real number
t : a point such as :
P + t (Q-P) ....... if a + b = 1 ... new notation : aP + bQ
<=> P + b (Q-P)
NB : convex combination <=> 0 <= t <= 1
if t1 + t2 + ... tn = 1
t1 P1 + t2 P2 + ... tn Pn <=> P1
+ t2 (P2 - P1) + ... tn (Pn - P1)
NB : convex affine combination <=>
0 <= ti <= 1
Slide 5 : Various other curiosities
Various other curiosities
Equation of a Line in an Affine Space defined by two point P and Q and t a
real
set of point of the form (1-t) P + t Q
Equation of a Plane in an Affine Space defined by three not collinear point
P, Q and R
set of point of the form (1-s) ((1-t) P + t Q) +s R
Vector and affine linear subspace are resp. vector and affine space
V : Non empty subset which is stable through the addition and the multiplication
by a real
A : such as the set of the difference between any element of A is a linear
vector subspace
Example
Vector subspace of R4
/ x
| y
| z
\ 0
Affine Subspace of R4 : standard affine 3 space
/ x / x1 - x2
| y v1 - v2 = | y1 - y2 belongs to the previous
| z | z1 - z2 vector subspace of R4
\ 1 \ 0
Slide 6 : Cartesian coordinate system
Cartesian coordinate system 2D
The cartesian plane : set of point labeled with coordinate (x, y) is an affine
space
Two usual cartesian reference frames
"Maths" frame
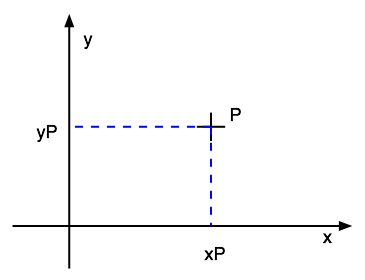
|
"Computer Graphics" frame
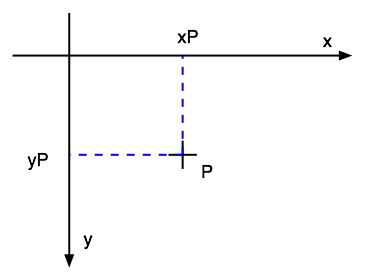
|
Slide 7 : Cartesian coordinate system 3D
Cartesian coordinate system 3D
The Cartesian space : set of point labelled with coordinate (x, y, z) is an
affine space
Two different orientations
3 fingers or thumb or corkscrew rules
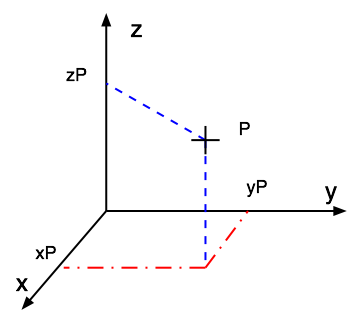
Right-handed system
Usual in Maths, Physics...
|
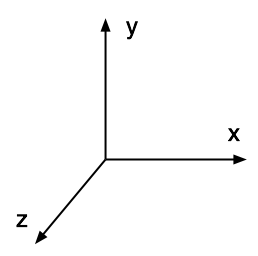 Java system
Java system
|
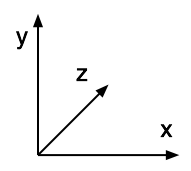 Left handed system
Left handed system
|
/ a1 / a2 / a2-a1
M | b1 P | b2 u = MP = | b2-b1
\ c1 \ c2 \ c2-c1
Slide 8 : Dot Product and Distance
Dot Product and Distance
a.k.a. Scalar Product
/ x1 / x2
u.v = | y1 . | y2 = x1.x2 + y1.y2 + z1.z2
\ z1 \ z2
Distance between M and P :
u = MP
Dist (M,P) = ||u|| = SquareRoot(u.u) = SquareRoot( (a2-a1)2
+ (b2-b1)2 + (c2-c1)2 )
v = 0 <=> ||v|| = 0 <=> v.v
= 0
/ a1 / a2 / a2-a1
M | b1 P | b2 u = MP = | b2-b1
\ c1 \ c2 \ c2-c1
Slide 9 : Dot Product and Angle
Dot Product and Angle
u.v = ||u||.||v||.cos(u,v)
if u and v are long enought... (u,v)
= acos(u.v / (||u||.||v||)
Trigonometrical circle
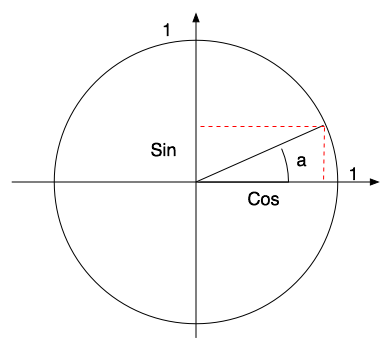
|
sin(0) = 0
sin(PI/2 rad) = 1
cos(0) = 1
sin(a) = opp/hyp
cos(a) = adj/hyp (Trigo + Thales)
if you know the cosinus, you don't know the sign of the angle !
u.v = 0 <=> (u,v) orthogonal, perpendicular (Maths)
u.v <= epsilon <=> (u,v) orthogonal, perpendicular (Computing)
(or u = 0, or v = 0 ...)
|
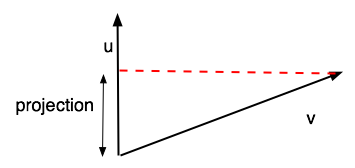
Lenght of the perpendical projection of v on u ??
Lenght = u.v / || v ||
|
 |
Slide 10 : Cross Product
Cross Product
a.k.a the vector product
/ x1 / x2 / y1.z2 - y2.z1
u x v = u ^ v = | y1 x | y2 = | x2.z1 - x1.z2
\ z1 \ z2 \ x1.y2 - x2.y1
u x v is a vector perpendicular to both u and v , which direction is given
by the usual right handed rule, and the lenght, by :
|| u x v || = || u || . || v || . sin (u,v)
now we are able to get the angle...
Slide 11 : Exercise from Last year Exam
Exercise from Last year Exam
Question 16 ( 8 marks ) :
Write an algorithm (Java-like pseudocode) that will calculate the point of
intersection of a ray (semi segment) and a triangle. The method should return
the status of the intersection (intersect or not, and, if not, why not ). If
it intersects, then the method should also return the coordinates of the intersection.
Use comments in your code to explain the algorithm.
The ray is defined by the origin point O and the direction vector V.
The triangle is defined by the 3 vertices P0, P1, P2.
Tip : if vertices A, B, C and D are on the same plane and if D = A + sAB +
tAC then D is inside triangle ABC if and only if s>=0, t>=0 and s+t <=
1
-
First compute the intersection point M between the ray and the plane of
the triangle
-
Then compute s and t such as M = P0 + s
P0P1 + t P0P2
-
Considering that M is inside the triangle if and only if s
>= 0, t >= 0 and s+t <= 1 draw your conclusion
Slide 12 : Exercise from Last year Exam
Exercise from Last year Exam
Question 16 ( 8 marks ) :
Write an algorithm (Java-like pseudocode) that will calculate the point of
intersection of a ray (semi segment) and a triangle. The method should return
the status of the intersection (intersect or not, and, if not, why not ). If
it intersects, then the method should also return the coordinates of the intersection.
Use comments in your code to explain the algorithm.
The ray is defined by the origin point O and the direction vector V.
The triangle is defined by the 3 vertices P0, P1, P2.
Tip : if vertices A, B, C and D are on the same plane and if D = A + sAB +
tAC then D is inside triangle ABC if and only if s>=0, t>=0 and s+t <=
1
-
First compute the intersection point M between the ray and the plane of
the triangle
-
Then compute s and t such as M = P0 + s
P0P1 + t P0P2
-
Considering that M is inside the triangle if and only if s
>= 0, t >= 0 and s+t <= 1 draw your conclusion
Next Week...

