Different coordinate systems = Different "Space"

Objects in the 3D scene and the scene itself are sequentially converted, or transformed, through five spaces when proceeding through the 3D pipeline. A brief overview of these spaces follows:

Model Space

where each model is in its own coordinate system, whose origin is some point on the model, such as the right foot of a soccer player model. Also, the model will typically have a control point or "handle". To move the model, the 3D renderer only has to move the control point, because model space coordinates of the object remain constant relative to its control point. Additionally, by using that same "handle", the object can be rotated.

World Space

where models are placed in the actual 3D world, in a unified world coordinate system. It turns out that many 3D programs skip past world space and instead go directly to clip or view space. The OpenGL API doesn't really have a world space.

View Space (also called Camera Space)

in this space, the view camera is positioned by the application (through the graphics API) at some point in the 3D world coordinate system, if it is being used. The world space coordinate system is then transformed, such that the camera (your eye point) is now at the origin of the coordinate system, looking straight down the z-axis into the scene. If world space is bypassed, then the scene is transformed directly into view space, with the camera similarly placed at the origin and looking straight down the z-axis. Whether z values are increasing or decreasing as you move forward away from the camera into the scene is up to the programmer, but for now assume that z values are increasing as you look into the scene down the z-axis. Note that culling, back-face culling, and lighting operations can be done in view space.
The view volume is actually created by a projection, which as the name suggests, "projects the scene" in front of the camera. In this sense, it's a kind of role reversal in that the camera now becomes a projector, and the scene's view volume is defined in relation to the camera. Think of the camera as a kind of holographic projector, but instead of projecting a 3D image into air, it instead projects the 3D scene "into" your monitor. 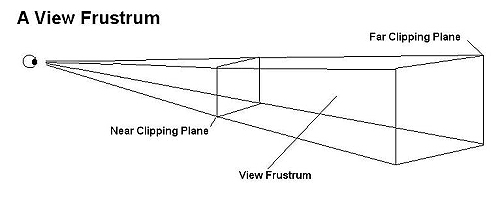The shape of this view volume is either rectangular (called a parallel projection), or pyramidal (called a perspective projection), and this latter volume is called a view frustum (also commonly called frustrum, though frustum is the more current designation).

The view volume defines what the camera will see, but just as importantly, it defines what the camera won't see, and in so doing, many objects models and parts of the world can be discarded, sparing both 3D chip cycles and memory bandwidth.
The frustum actually looks like an pyramid with its top cut off. The top of the inverted pyramid projection is closest to the camera's viewpoint and radiates outward. The top of the frustum is called the near (or front) clipping plane and the back is called the far (or back) clipping plane. The entire rendered 3D scene must fit between the near and far clipping planes, and also be bounded by the sides and top of the frustum. If triangles of the model (or parts of the world space) falls outside the frustum, they won't be processed. Similarly, if a triangle is partly inside and partly outside the frustrum the external portion will be clipped off at the frustum boundary, and thus the term clipping. Though the view space frustum has clipping planes, clipping is actually performed when the frustum is transformed to clip space.

Clip Space

Similar to View Space, but the frustum is now "squished" into a unit cube, with the x and y coordinates normalized to a range between –1 and 1, and z is between 0 and 1, which simplifies clipping calculations. The "perspective divide" performs the normalization feat, by dividing all x, y, and z vertex coordinates by a special "w" value, which is a scaling factor that we'll soon discuss in more detail. The perspective divide makes nearer objects larger, and farther objects smaller as you would expect when viewing a scene in reality.

Screen Space

where the 3D image is converted into x and y 2D screen coordinates for 2D display. Note that z and w coordinates are still retained by the graphics systems for depth/Z-buffering (see Z-buffering section below) and back-face culling before the final render. Note that the conversion of the scene to pixels, called rasterization, has not yet occurred.

Because so many of the conversions involved in transforming through these different spaces essentially are changing the frame of reference, it's easy to get confused. Part of what makes the 3D pipeline confusing is that there isn't one "definitive" way to perform all of these operations, since researchers and programmers have discovered different tricks and optimizations that work for them, and because there are often multiple viable ways to solve a given 3D/mathematical problem. But, in general, the space conversion process follows the order we just described.
To get an idea about how these different spaces interact, consider this example:
Take several pieces of Lego, and snap them together to make some object. Think of the individual pieces of Lego as the object's edges, with vertices existing where the Legos interconnect (while Lego construction does not form triangles, the most popular primitive in 3D modeling, but rather quadrilaterals, our example will still work). Placing the object in front of you, the origin of the model space coordinates could be the lower left near corner of the object, and all other model coordinates would be measured from there. The origin can actually be any part of the model, but the lower left near corner is often used. As you move this object around a room (the 3D world space or view space, depending on the 3D system), the Lego pieces' positions relative to one another remain constant (model space), although their coordinates change in relation to the room (world or view spaces). In some sense, 3D chips have become physical incarnations of the pipeline, where data flows "downstream" from stage to stage. It is useful to note that most operations in the application/scene stage and the early geometry stage of the pipeline are done per vertex, whereas culling and clipping is done per triangle, and rendering operations are done per pixel. Computations in various stages of the pipeline can be overlapped, for improved performance. For example, because vertices and pixels are mutually independent of one another in both Direct3D and OpenGL, one triangle can be in the geometry stage while another is in the Rasterization stage. Furthermore, computations on two or more vertices in the Geometry stage and two or more pixels (from the same triangle) in the Rasterzation phase can be performed at the same time.
Another advantage of pipelining is that because no data is passed from one vertex to another in the geometry stage or from one pixel to another in the rendering stage, chipmakers have been able to implement multiple pixel pipes and gain considerable performance boosts using parallel processing of these independent entities. It's also useful to note that the use of pipelining for real-time rendering, though it has many advantages, is not without downsides. For instance, once a triangle is sent down the pipeline, the programmer has pretty much waved goodbye to it. To get status or color/alpha information about that vertex once it's in the pipe is very expensive in terms of performance, and can cause pipeline stalls, a definite no-no.

ExtremeTech 3D Pipeline Tutorial
June, 2001
By: Dave Salvator

extract from http://www.extremetech.com/