Spline

Types of Curves : Explicit (z = f( x, y)), Implicit (f( x, y, z) = 0), Parametric (x = f(u,v), y = g(u,v)...)

Spline : Parametric, Control Points, Knots

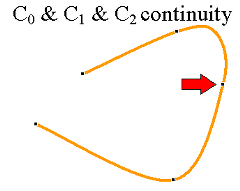
Zero order parametric continuity

The curves meet

First order parametric continuity

the tangents are shared

Second order parametric continuity

the"speed" is the same before and after

animation paths...

A Spline Curve : Any Composite curve formed with polynomial sections satifying specified continuity conditions at the boundary of the pieces.

The whole story of polynomial slines is deriving their coefficients by satisfying the constraints set by the knots and continuity conditions C0, C1, continuity at the extremities.

Cubic Hermite Spline :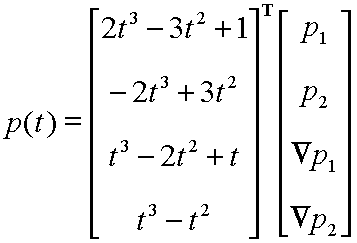

Bézier Curve

A Cubic Bezier Spine has four control points, two of which are knots.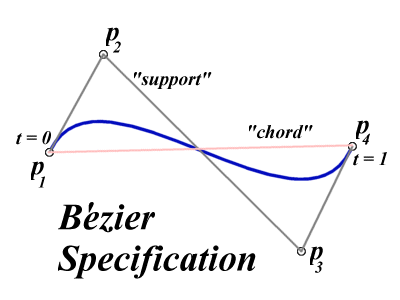

Some of theses properties may sound somewhere obvious, but they are presented here because they are still valid for Bézier curves of higher degree

A Bézier cure is a polynomial.

The degree of the polynomial is always one less than the number of control points. In computer graphics, we generally use degree 3. Quadratic curves are not flexible enough and going above degree 3 gives rises to complications and so the choice of cubics is the best compromise for most computer graphics applications.

The curves follows the shape of the control point polygon.

It is constrained within the convex hull formed by the control points.

The control points do not exert 'local' control.

Moving any control point affects all of the curve to a greater or lesser extent. All the basis functions are everywhere non-zero except at the point u = 0 and u = 1

The first and last control points are the end points of the curves segment

The tangent vectors to the curve at the end points are coincident with the first and last edge of the control point polygon.

Moving the control points alters the magnitude and direction of the tangent vectors

This is the basis of the intuitive 'feel' of a Bézier curve interface.

Variation diminishing property

The curve does not oscillate about any straight line more often than the control point polygon

Affine transformation compatibility

The curve is transformed by applying any affine transformation (that is, any combination of linear transformations) to its control point representation. The curve is invariant (does not change shape) under such a transformation.