First Assignment
"If you please, draw me a fractal (*)."
In this assignment you will be asked to draw a Sierpinski Gasket and a Sierpinski Carpet fractal. The drawing of this sort of fractal is based on recursion. By recursion we mean something that uses itself to define itself. E.g. "GNU acronym stands for: 'GNU is Not Unix'". That first example is of course a bad hacker joke. More Seriously, you can define the mathematical value of factorial n (which is n(n-1)(n-2)... 2 * 1 ) by :
- factorial(n) = n * factorial(n -1) if n > 0
- factorial(0) = 1
- Have a look at Exercise 2 and its tips about recursion
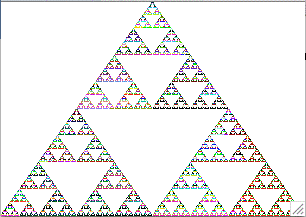
Find in the attached paper the definition of a Sierpinski Gasket. Here is a general idea of what it looks like when starting the iteration with a rectangle:
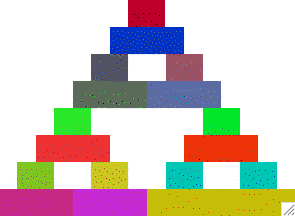 level 3 |
|
Ground Rules for all projects:
- The design and coding must be your own.
- Don't use code from previous semesters.
- Cite any models, images, ideas, or algorithms that you do not develop yourself.
- Project is due before midnight of the day indicated : 28 August 2001.
- Please read this text through to the end before touching any keyboard.
- Then before beginning the project, have a look at this document on the web
page : you will found some useful links like the one to the README file model.
To submit a project...
you should put altogether, in a directory called COMPXXXX_A1_UstudentID...
(Where XXXX is the right lecture code (6461 or 4610) and 'studentID'... your student ID !)
- Your well commented Java source file(s)
- Your compiled classes
- The documentation from javadoc
- A 'README.html' HTML file that should summarise all what is available in
your directory and how to use your program (and especially the in line option)
Here is its README.html file template
Use the jar command to put your directory into a single jar file based on the same name and mail this file to pascal.vuylsteker@anu.edu.au
cd .. (go to the directory in which your COMPXXXX_A1_UstudentID is located)
jar cvf COMPXXXX_A1_UstudentID.jar COMPXXXX_A1_UstudentID/
Mail the file (COMPXXXX_A1_UstudentID.jar) as a attached document. Be
sure that the title of your mail is 'CGA1:COMPXXXX_A1_UstudentID.jar'
The minimum requirements
Your project should be composed of, at least, the following :
(1) One abstract class. You should put (declare and or implement) as many as
possible things that are common to what is necessary to write a recursive fractal
in that class. This class could, for instance, extend a JPanel ( or a JFrame,
depending on the architecture you choose). One could imagine that the method
that make the class 'abstract', is for instance, the one that will draw a given
level of a given type of fractal ( abstract protected void buildElement(double
xmin, double ymin, double xmax, double ymax, int level, Color color, Graphics
g) for instance);
(2) Two public classes that will implement respectively a Sierpinski Gasket and a Sierpinski Carpet.
(3) One public class, whose name will be "Assignment" and that will contain the "main method" in such a way to test your project, I will only need to call 'java Assignment [command line arguments]' to run it. Because yours classes will be well documented, I should be able to write that "Assignment" class by myself without to much work.
(4) You will explain the use of the arguments in your README file but the two first one will be gasket|carpet IterationNumber
Eg : java Assignment gasket 7
will draw the 7th level of a Sierpinski Gasket
(5) Remember that sometime, users may be dumb and may not use the right number of of argument.
(6) Remember that again, users may be dumb and could use a very high Iteration Number. It could be a good idea to have 2 trivial criteria to end the recursion. One is the number of iterations, the other one is...(this is the sort of thing -amongst others- that should appear either in your code comments and in the README file)
(7) One peculiarity of these fractal displays is that the panel should be resizable (whenever the size of the window is changed by the user, the fractal should be redrawn in order to fit in all the available space).
Optional stuff that will impress:
You should do at least one of theses option to get the maximum mark
- Interactive change (GUI) of the number of level of iteration
- Interactive change (GUI) of the type of fractal
- Use of colour to make the fractal more alluring
- Use the same abstract to display a Koch Snowflake fractal
- By default, it is asked to draw only the final stage of the recursion, but you could add an option to draw one after the other all the intermediate levels
(*) If you didn't know that the original quotation was about a sheep, you should perhaps first read "The little prince" story before beginning to do computer graphics.