MidPoint algorithm (2)

What we'd like to do is to use this discriminating function to maintain our trajectory of drawn pixels as close as possible to the desired circle. Luckily, we can start with a point on the circle, (x0, y0+r) (or (0, r) in our adjusted coordinate system). As we move along in steps of x we note that the slope is less than zero and greater than negative one at points in the direction we're heading that are near our known point on a circle. Thus we need only to figure out at each step whether to step down in y or maintain y at each step.

 

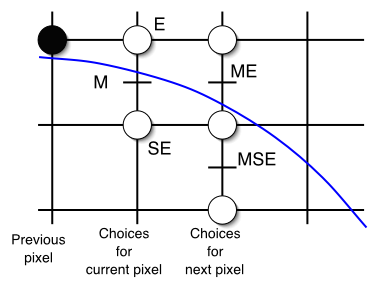
We will compute points between x=0 and x=y and then draw the 8 matching points

In that area, the slope of the curve is between 0 and -1

From each step/point (x, y), the next one is either (x+1, y) or (x+1, y-1)

We decide about which one by looking at the midpoint M

  • M inside (f<0) => next point is E

  • M ouside (f>0) => next point is SE

 

Dold = f( x + 1, y - 1/2) = ( x + 1 )2 + ( y -1/2 )2 - r2 = f(x,y) + 2x - y + 5/4

if Dold < 0, E is chosen (y)
Dnew = f(x + 2, y -1/2) = ( x + 2 )2 + ( y -1/2 )2 - r2 = f(x,y) + 4x -y + 3 + 5/4
Dnew = Dold + 2x + 3 = Dold + 2(x+1) +1

if Dold >0, ES is chosen (y-1)
Dnew = f(x + 2, y - 3/2) = ( x + 2 )2 + ( y - 3/2 )2 - r2 = f(x,y) + 4x -3y + 5 + 5/4
Dnew = Dold + 2x -2y + 5 = Dold + 2((x+1) -(y-1) + 1)

D0 = f(1, r-1/2) = 5/4 - r ...not an inger
Lets change every where D by P = D - 1/4
P0 = 1 - r , and because increment are always integer, P < -1/4 <=> P < 0

 

        int x = 0;
        int y = radius;
        int p = 1 - radius;
        circlePoints(xCenter, yCenter, x, y, pix);
        while (x < y) {
            x++;
            if (p < 0) {
                p += 2*x+1;
            } else {
                y--;
                p += 2*(x-y+1);
            }
            circlePoints(xCenter, yCenter, x, y, pix);
        }