MidPoint algorithm

Let's simplify the function evaluation that takes place on each iteration of our circle-drawing algorithm

So our next objective is to simplify the function evaluation that takes place on each iteration of our circle-drawing algorithm. All those multiplies and square-root evaluations are expensive. We can do better.

We translate our coordinate system so that the circle's center is at the origin

One approach is to manipulate the circle equation slightly. First, we translate our coordinate system so that the circle's center is at the origin (the book leaves out this step), giving:

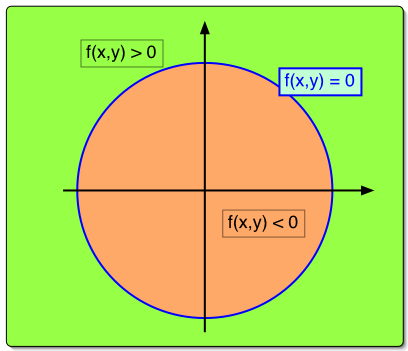
( ( x + x0 ) - x0 )2 + ( ( y - y0 ) - y0 )2 = r2

We simplify and make the equation homogeneous

Next, we simplify and make the equation homogeneous (i.e. independent of a scaling of the independent variables; making the whole equation equal to zero will accomplish this) by subtracting r² from both sides.

x2 + y2 - r2 = 0

We can regard this expression as a function in x and y.

Discriminating function : partition the domain, into one of three categories

f( x, y ) = x2 + y2 - r2

Functions of this sort are called discriminating functions in computer graphics. They have the property of partitioning the domain, pixel coordinates in our case, into one of three categories. When f(x,y) is equal to zero the point lies on the desired locus (a circle in this case), when f(x, y) evaluates to a positive result the point lies one side of the locus, and when f(x,y) evaluates to negative it lies on the other side.