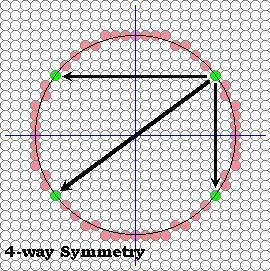
Let's use 2 symmetries : Symmetry 4
|
 |
Looks Fine in areas where only one pixel is required for each column
We could compute the derivative (i.e. the local slope)
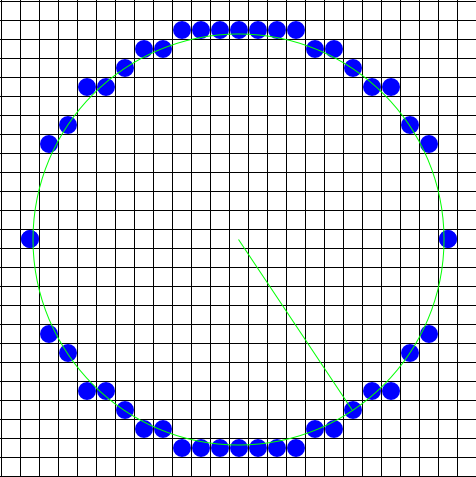
A circle : a great deal of symmetry
Already : two pixels for each function evaluation
As you can see the circles look fine in areas where only one pixel is required for each column, but in areas of the circle where the local slope is greater the one the circle appears discontinuous (where have we seen this before?).
We could take the approach of computing the derivative (i.e. the local slope) of the function at each point and then make a decision whether to step in the x direction or the y direction. But, we will explore a different approach here.
A circle exhibits a great deal of symmetry. We've already exploited this somewhat by plotting two pixels for each function evaluation; one for each possible sign of the square-root function. This symmetry was about the x-axis. The reason that a square-root function brings out this symmetry results from our predilection that the x-axis should be used as an independent variable in function evaluations while the y-axis is dependent. Thus, since a function can yield only one value per member of the domain, we are forced to make a choice between positive and negative square roots. The net result is that our simple circle-drawing algorithm exploits 2-way symmetry about the x-axis.
Obviously, a circle has a great deal more symmetry. Just as every point above an x-axis drawn through a circle's centre has a symmetric point an equal distance from, but on the other side of the x-axis, each point also has a symmetric point on the opposite side of a y-axis drawn through the circle's centre.