AntiAliasing
Back in the 1930's ... Nyquist sampling theories
To accurately reproduce an analog waveform, you must digitally sample an analog signal at a rate at least twice its highest frequency to be able to represent the signal in the digital domain with a high level of accuracy.
n sample >= 2 x nanalog
insufficient sampling rate == > aliasing
Aliasing is a potential problem whenever an analog signal is point sampled to convert it into a digital signal. It can occur in audio sampling, for example, in converting music to digital form to be stored on a CD-ROM or other digital device. Aliasing happens whenever an analog signal is not sampled at a high enough frequency. In audio, Aliasing manifests itself in the form of spurious low frequencies. An example is shown below of two sin waves.
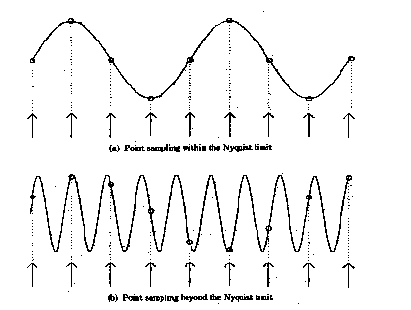
Image Reference : Robert L. Cook, "Stochastic Sampling and Distributed Ray Tracing", An Introduction to Ray Tracing, Andrew Glassner, ed., Academic Press Limited, 1989.
In the top sin wave, the sampling is fast enough that a reconstructed signal (the small circles) would have the same frequency as the original sin wave. In the bottom wave, with a higher frequency but the same point sampling rate, a reconstructed signal (the small circles) would appear to be a sin wave of a lower frequency, i.e., an aliased signal.
From Point Sampling Theory it turns out that to accurately reconstruct a signal, the signal must be sampled at a rate greater than or equal to two times the highest frequency contained in the signal. This is called the Nyquist Theorem and the highest frequency that can be accurately represented with a given sampling rate is called the Nyquist limit. For example, to produce a music CD-ROM the analog signal is sampled at a maximum rate of 44 Khz, therefore the highest possible audio frequency is 22khz. Any audio frequencies greater than 22Khz must be removed from the input signal or they will be aliased, i.e., appear as low frequency sounds.
Aliasing occurs in computer graphics, since we are point sampling an analog signal. The mathematical model of an image is a continuous analog signal which is sampled at discrete points (the pixel positions). When the sampling rate is less than Nyquist Limit then there are aliasing artifacts that are called "jaggies" in computer graphics. In general, aliasing is when high frequencies appear as low frequencies which produce regular patterns easy to see.
Most things in the real world are continuous
Everything in a computer is discrete
The process of mapping a continuous function to a discrete one is called sampling
The process of mapping a continuous variable to a discrete one is called quantization
When we represent or render an image using a computer we must both sample and
quantize
Picturing an Image as a 2D Function
An ideal image can be viewed as a function, I(x, y), that gives an intensity
for any given coordinate (x, y). We could plot this function as a height field.
This plot would lowest at dark points in the image and highest at bright points.
Most of the functions that we encounter are analytic and, therefore, can be
expressed as simple algebraic relations. An image, in general, cannot representaed
in such a simple form. Instead, we represent images as tabulated functions.
So how do we fill this table?

When a continuous image is multiplied by a sampling grid a discrete set of points are generated. These points are called samples. These samples are pixels. We store them in memory as arrays of numbers representing the intensity of the underlying function.
The same analysis can be applied to geometric objects:
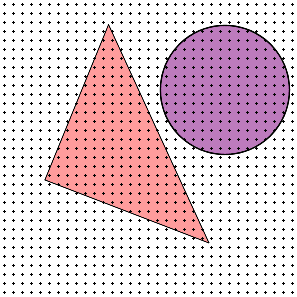
Sampling Theorem
In order to have any hope of accurately reconstructing a function from a periodically sampled version of it, two conditions must be satisfied:
- The function must be bandlimited.
- The sampling frequency, fs, must
be at least twice the maximum
frequency, fmax, of the function.
In practice:
- "Jaggies" are aliasing
- Both of the techniques discussed are used
- Super-sampling (more samples than pixels)
- Low-pass prefiltering (averaging of super-samples)