Bernstein-Bezier Formulation of Bezier Curve (Spline)

The Bernstein-Bezier formulation is based on the subdivision property of Bezier curves.

The subdivision property completes the definition of the spacing of the control points.

The subdivision construction is:

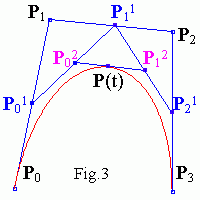
Draw lines connecting the control points, and then recursively draw lines between the midpoints of those lines for a total of n-2 iterations, where n is the degree of the Bezier curve (Figure 3.1.). For a cubic Bezier curve, n=3, so there is just one subdivision.

Points P₀ , P₀¹ , P₀² , P(t) and P(t) , P₁² , P₂¹ , P₃ are control points of new small splines again.

To learn more..."Cubic Bezier Patches Used to Draw Utah Teapot"