8-way symmetry algorithm
Symmetry about the pair of lines with slopes of one and minus one
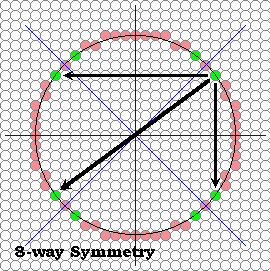
We can find any point's symmetric complement about these lines by permuting the indices. For example the point (x,y) has a complementary point (y,x) about the line x=y. And the total set of complements for the point (x,y) are
get point's symmetric complement about these lines by permuting the indices
:
{(x,-y), (-x,y), (-x,-y), (y,x), (y,-x), (-y,x),(-y,-x)}
algorithm loops over one-eighth of the circle from the top to the right by 45 degrees
The following routine takes advantage of this 8-way symmetry. The algorithm loops over one-eighth of the circle. Specifically, it starts at the top of the circle and goes to the right by 45 degrees, where the slope of a radial line is 1. Thus, the stopping state is crossing the x=y line.
public void circleSym8(int xCenter, int yCenter, int radius, Color c)
{
int pix = c.getRGB();
int x, y, r2;
r2 = radius * radius;
raster.setPixel(pix, xCenter, yCenter + radius);
raster.setPixel(pix, xCenter, yCenter - radius);
raster.setPixel(pix, xCenter + radius, yCenter);
raster.setPixel(pix, xCenter - radius, yCenter);
x = 1;
y = (int) (Math.sqrt(r2 - 1) + 0.5);
while (x < y) {
raster.setPixel(pix, xCenter + x, yCenter + y);
raster.setPixel(pix, xCenter + x, yCenter - y);
raster.setPixel(pix, xCenter - x, yCenter + y);
raster.setPixel(pix, xCenter - x, yCenter - y);
raster.setPixel(pix, xCenter + y, yCenter + x);
raster.setPixel(pix, xCenter + y, yCenter - x);
raster.setPixel(pix, xCenter - y, yCenter + x);
raster.setPixel(pix, xCenter - y, yCenter - x);
x += 1;
y = (int) (Math.sqrt(r2 - x*x) + 0.5);
}
if (x == y) {
raster.setPixel(pix, xCenter + x, yCenter + y);
raster.setPixel(pix, xCenter + x, yCenter - y);
raster.setPixel(pix, xCenter - x, yCenter + y);
raster.setPixel(pix, xCenter - x, yCenter - y);
}
}
8 points for every function evaluation
Routine should be approximately 4-times faster than our initial circle-drawing algorithm
So now we get 8 points for every function evaluation, and this routine should be approximately 4-times faster than our initial circle-drawing algorithm. What's going on with the four pixels that are set outside the loop (both at the top and bottom)? Didn't I say that every point determines 7 others?
And It Works ! Without any special code to test for the slope ??? Not Really
It seems suddenly that our circles appear continuous, and we added no special code to test for the slope. Symmetry has come to our rescue. (Actually, symmetry is also what saved us on lines, if you think about it.)