The Rendering Equation (à la Kajiya - Siggraph 86)

An attempt to unify rendering so that all rendering had a basic model as a basis.

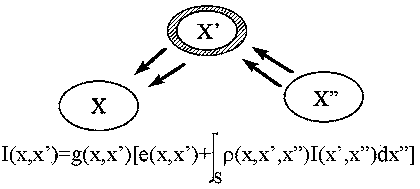
 where:

• I ( x , x' ) is the intensity of light passing from point x' to point x.

• g ( x , x' ) is the visibility between x and x'. If they are occluded, this is zero, otherwise it varies as the inverse square of the distance between them. The part right to that expression is the : the "unoccluted two point transport intensity".

• e ( x , x' ) is the transfer emittance from x' to x. It is related to the intensity of any light self emitted by point x' in the direction of x

• r ( x , x' , x'' ) is the scattering term or bidirectional reflectivity with respect to directions x' and x''. It is the intensity of the energy scattered towards x by a surface point located at x' arriving from point or directions x''. The "Unoccluted three-point transport reflectance" Related to the BRDF

• S represents all points on all surfaces in the scene

• i.e. the transport intensity from x' to x is the sum of emitted light from x' to x and all light from x'' that eventually gets to x through x'.

This is of course a recursive definition !

Complexity => practical solution are aproximations

View Independant statement of the problem

• solutions can be view independant (radiosity) or not (raytracing)

we can rewrite this equation as
where R is the linear integral operator

rearranging terms gives: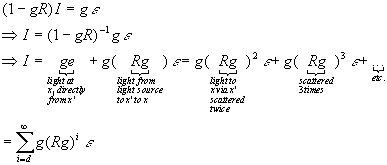

.

Local Reflection Models

.

only first 2 terms are used

X is the eyepoint

the g(epsilon) term is non-zero only for light sources

R₁ operates on (epsilon) rather than g, so shadows are not computed

Basic Ray Tracing

Radiosity

by performing transformations outlined on page 293 of the text, we get

• dB(x') is the radiosity of surface element dx'
• p₀ is p( x , x' , x'' ) and is constant
• H(x') is the energy incident on the surface element dx'

The Extended Two-Pass Algorithm (Sillion 1989)

.

p(x, x', x'') = pd(x') + ps(x, x', x'')

bidirectional   diffuse    specular
reflectivity
  function