Path Notation (2)

An accurate method must handle all four types : L (D|S|G)* E

Local Illumination Model : L (D|S|G) E

First, let’s introduce some notation for paths. Each path is terminated by the eye
and a light.
E - the eye.
L - the light.
Each bounce involves an interaction with a surface. We characterize the interaction
as either reflection or transmission. There are different types of reflection and
transmission functions. At a high-level, we characterize them as
D - diffuse reflection or transmission
G - glossy reflection or transmission
S - specular reflection or refraction
Diffuse implies that light is equally likely to be scattered in any direction. Specular
implies that there is a single direction; that is, given an incoming direction there is
a unique outgoing direction. Finally, glossy is somewhere in between.
Particular ray-tracing techniques may be characterized by the paths that they
consider.
Appel Ray casting: E(D | G)L
Whitted Recursive ray tracing: E[S*](D | G)L
Kajiya Path Tracing: E[(D | G | S) + (D | G)]L
Goral Radiosity: ED*L
The set of traced paths are specified using regular expressions, as was first proposed
by Shirley. Since all paths must involve a light L, the eye E, and at least one
surface, all paths have length at least equal to 3.
A nice thing about this notation is that it is clear when certain types of paths
are not traced, and hence when certain types of light transport is not considered
by the algorithm. For example, Appel’s algorithm only traces paths of length 3,
ignoring longer paths; thus, only direct lighting is considered. Whitted’s algorithm
traces paths of any length, but all paths begin with a sequence of 0 or more mirror
reflection and refraction steps. Thus, Whitted’s technique ignores paths such as
the following EDSDSL or E(D | G)* L. Distributed ray tracing and path tracing
includes multiple bounces involving non-specular scattering such as E(D | G)* L.
However, even these methods ignore paths of the form E(D | G)S* L; that is, multi-ple
specular bounces from the light source as in a caustic. Obviously, any technique
that ignores whole classes of paths will not correctly compute the solution to the
rendering equation.

---

Radiosity : L D* E

• very good at diffuse - diffuse

• a two-pass algorithm can include specular to diffuse

• radiosity is view-independent, specularity is not

Whitted Recursive Ray tracing: E S* (D|G) L   

• specular to specular handled well

• diffuse to specular handled somewhat

• specular to diffuse can be included using a two-pass method or by backwards ray tracing

Combining Radiosity and Ray Tracing

• A two-pass approach

  • Pass 1: enhanced radiosity to account for diffuse to diffuse and specular to diffuse

  • Pass 2: diffuse to specular and specular to specular using enhanced ray tracing

• Why two passes?

  • view-independent specularity and view-dependent diffuse computations are too expensive

  • a view-independent diffuse computation followed by a view-dependent specular computation is doable

 

---

First Pass - formalized by Rushmeier and Torrance

• accounts for ideal specular and ideal diffuse reflection and transmission
• number of specular surfaces should be small
• derive the radiosity equation in terms of intensities
  
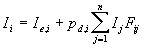
  for an ideal diffuse surface
  
  
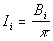
• This equation is extended to account for diffuse to specular transfer and transmission

Diffuse Transmission

• (through a light shade, for example)
• assuming no specular interaction, we get
  
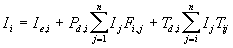
  where I_d,i is the diffuse transmittance for patch i and T_ij is transmission form factor
• T_ij
  • accounts for interaction between ideal diffuse surfaces due to transmission
  • called backwards diffuse form factor
  • T_ij computed by placing a hemisphere over the back side of the surface, then performing the same computation as for F_ij.

Specular Transmission

• place a constraint that no two specular surfaces can see each other
• then
  
  
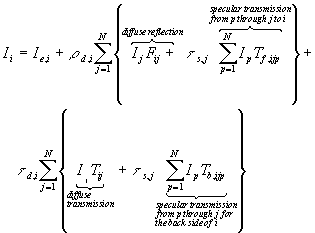
• T_f,ijp is the window form factor and accounts for the energy leaving patch p that is specularly transmitted through j and reaches i
• [image: shows three patches p floating above a patch j which is floating above patch i. Caption reads: Patches p visible to i through j ]
• T_b,ijp is a similar quanitity that accounts for transmission from p through j to the back side of i
• These T form factors can be computed with the hemicube, just as the F form factors are.
• [image: shows a patch i with a hemicube sitting atop it. Floating above the hemicube is patch j. Above patch j is patch p. T_f,ijp appears to be an area on the hemicube, representing what is visible of patch p through patch j onto patch i. ]

Specular Reflection

• use the same constraint that no two specular surfaces can see each other, but contribute to interaction between patches.
• mirror form factors
• [image: Patch p is a mirror. To the right of patch p, we have the real environment, which consists of patch j and patch i. To the left of patch p, we have a virtual environment representing what is seen in p's reflection. Patch j', the reflection of patch j, sits in the virtual environment. ]
• 
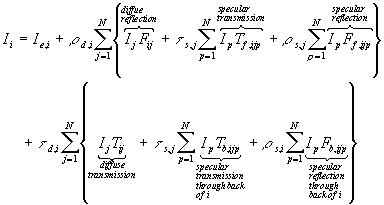
• F_f,ijp is the forward mirror form factor
• F_b,ijp is the backward mirror form factor
• using the mirror approach with virtual space, the specular patch is treated as a specular tranmittor that receives light from the virtual patch.
• mirror form factors are computed just as window form factors, except virtual surfaces are used.

With these extensions, we can now account for:

• diffuse - diffuse (regular radiosity)
• specular - diffuse (extended radiosity à la Rushmeier & Torrance

Once this pass is complete, we then perform the 2^nd pass to compute specular - specular and diffuse - specular

Specular - specular is given by ray tracing

For diffuse - specular, we would need to send out many rays from the point through the hemisphere around the point, weight the rays by the bidirectional specular reflectivity, then sum them together.

• [image: too complicated to describe, but you can look at the photocopied notes if you have them ]
• the reflection frustrum is a square pyramid
• the end of the pyramid is divided into n x n pixels (typically very low resolution - e.g. 10 x 10)
• Z-buffer is used on that face to determine visible surfaces
• The specular contribution is the intensities of the patches seen through the frustrum (as computed in pass 1)
• if the patch seen through the frustrum is specular, the process is recursively repeated
• the incoming intensities can be weighted to approximate the specular spread\