| Class Hierarchy | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Class Hierarchy | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The Group node object is a general-purpose grouping node.
Group nodes have exactly one parent and an arbitrary number of children that
are rendered in an unspecified order (or in parallel). Null children are allowed;
no operation is performed on a null child node. Operations on Group node objects
include adding, removing, and enumerating the children of the Group node. The
subclasses of Group node add additional semantics.
| Method | Default |
|---|---|
| Group( ) | - |
|
void addChild( Node child ) Appends the specified child to this node's list of children. |
None |
|
void setChild( Node child, int index ) Replaces the node's specified child with the child provided. |
None |
|
void insertChild( Node child, int index ) Inserts the node's specified child at the specified index location. |
None |
|
getChild(int index) Returns the node's index selected child. |
None |
|
void removeChild( int index ) Removes the node's child at the specified index location. |
None |
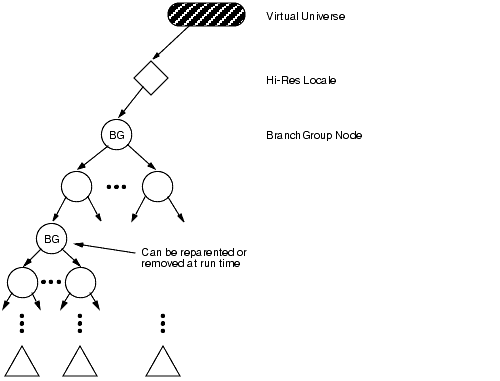
The BranchGroup serves as a pointer to the root of a scene graph branch; BranchGroup objects are the only objects that can be inserted into a Locale's set of objects. A subgraph, rooted by a BranchGroup node can be thought of as a compile unit.
The following things may be done with BranchGroup:
Note that that if a BranchGroup is included in another subgraph, as a child of some other group node, it may not be attached to a Locale.
| BranchGroup Class Methods | Default |
|---|---|
| BranchGroup( ) | - |
| void compile( ) | None |
| void detach( ) | None |
Locale locale = new Locale( universe );
Shape3D shape = new Shape3D( geom, app );
. . .
BranchGroup branch = new BranchGroup( );
branch.addChild( shape );
branch.compile( );
. . .
locale.addBranchGraph( branch );
The OrderedGroup node guarantees that Java 3D will render its children in their index order. Only the OrderedGroup node and its subclasses make any use of the order of their children during rendering.
Shape3D encompass = new Shape3D( geom, app );
Shape3D decal1 = new Shape3D( geom1, app1 );
Shape3D decal2 = new Shape3D( geom2, app2 );
. . .
DecalGroup decals = new DecalGroup( );
decals.addChild( encompass );
decals.addChild( decal1 );
decals.addChild( decal2 );
The DecalGroup node is a subclass of the OrderedGroup node. The DecalGroup node is an ordered group node used for defining decal geometry on top of other geometry. The DecalGroup node specifies that its children should be rendered in index order and that they generate coplanar objects. Examples include painted decals or text on surfaces and a checkerboard layered on top of a table.
The first child, at index 0, defines the surface on top of which all other children are rendered. The geometry of this child must encompass all other children; otherwise, incorrect rendering may result. The polygons contained within each of the children must be facing the same way. If the polygons defined by the first child are front facing, then all other surfaces should be front facing. In this case, the polygons are rendered in order. The renderer can use knowledge of the coplanar nature of the surfaces to avoid Z-buffer collisions. (If, for example, the underlying implementation supports stenciling or polygon offset, then these techniques may be employed.) If the main surface is back facing, then all other surfaces should be back facing and need not be rendered (even if back-face culling is disabled).
Note that using the DecalGroup node does not guarantee that Z-buffer collisions are avoided. An implementation of Java 3D may fall back to treating DecalGroup node as an ordinary OrderedGroup node.
The Switch group node allows a Java 3D application to choose dynamically among a number of subgraphs. The Switch node contains an ordered list of children and a switch value. The switch value determines which child or children Java 3D will render. Note that the index order of children is used only for selecting the appropriate child or children-it does not specify rendering order.
These values, when used in place of a nonnegative integer index value, indicate which children of the Switch node are selected for rendering. A value of CHILD_NONE indicates that no children are rendered. A value of CHILD_ALL indicates that all children are rendered, effectively making this Switch node operate as an ordinary Group node. A value of CHILD_MASK indicates that the childMask BitSet is used to select the children that are rendered.
public class BitSet
extends Object
implements Cloneable, Serializable
This class implements a vector of bits that grows as needed. Each component
of the bit set has a boolean value. The bits of a BitSet are indexed by nonnegative
integers. Individual indexed bits can be examined, set, or cleared. One BitSet
may be used to modify the contents of another BitSet through logical AND, logical
inclusive OR, and logical exclusive OR operations.
By default, all bits in the set initially have the value false.
| Method | Default |
|---|---|
| Switch( ) | - |
| void setWhichChild( int index ) | CHILD_NONE |
| void setChildMask( BitSet mask ) | None |
Shape3D first = new Shape3D( geom1, app1 );
Shape3D second = new Shape3D( geom2, app2 );
Shape3D third = new Shape3D( geom3, app3 );
. . .
Switch group = new Switch( );
group.addChild( first );
group.addChild( second );
group.addChild( third );
. . .
setWhichChild(1);
| Method | Default |
|---|---|
| SharedGroup( ) | - |
| void compile( ) | None |
| Method | Default |
| Link( ) | - |
| Link( SharedGroup group ) | - |
| void setSharedGroup( SharedGroup group ) | None |
TransformGroup groupA = new TransformGroup( ); TransformGroup groupB = new TransformGroup( ); Shape3D shape1 = new Shape3D( geom1, app1 ); Shape3D shape2 = new Shape3D( geom2, app1 ); . . . SharedGroup shared = new SharedGroup( ); shared.addChild( shape1 ); shared.addChild( shape2 ); shared.compile( ); . . . Link linkA = new Link( shared ); Link linkB = new Link( shared ); . . . groupA.addChild( linkA ); groupB.addChild( linkB );
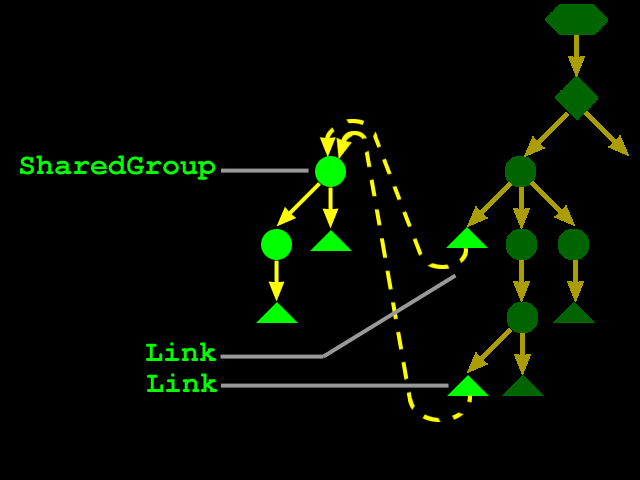
The TransformGroup node specifies a single spatial transformation-via
a Transform3D object -that can position, orient, and scale all of its children.
The specified transformation must be affine. Further, if the TransformGroup
node is used as an ancestor of a ViewPlatform node in the scene graph, then
the transformation must be congruent-only rotations, translations, and uniform
scales are allowed in a direct path from a Locale to a ViewPlatform node. A
BadTransformException is thrown if an attempt is made to specify an illegal
transform.
------------------------------------------------------------------------
Note: Even though arbitrary affine transformations are allowed, better performance
will result if all matrices within a branch graph are congruent-containing only
rotations, translation, and uniform scale.
------------------------------------------------------------------------
The effects of transformations in the scene graph are cumulative. The concatenation
of the transformations of each TransformGroup in a direct path from the Locale
to a Leaf node defines a composite model transformation (CMT) that takes points
in that Leaf node's local coordinates and transforms them into Virtual World
(Vworld) coordinates. This composite transformation is used to transform points,
normals, and distances into Vworld coordinates. Points are transformed by the
CMT. Normals are transformed by the inverse-transpose of the CMT. Distances
are transformed by the scale of the CMT. In the case of a transformation containing
a nonuniform scale or shear, the maximum scale value in any direction is used.
This ensures, for example, that a transformed bounding sphere, which is specified
as a point and a radius, continues to enclose all objects that are also transformed
using a nonuniform scale.
| Method | Default/possible values |
|---|---|
| public TransformGroup( ) | Identity |
| public TransformGroup(Transform3D t1) | |
| public void setTransform( Transform3D xform ) | Identity |
| public void getTransform(Transform3D t1) | |
| public final void setCapability(int bit) (from SceneGraphObject) | ALLOW_TRANSFORM_READ / ALLOW_TRANSFORM_WRITE |
|
public final boolean getCapability(int bit) |
Just stay with simple combination and you won't have any trouble
(§ Homonym: sheer)
1. A machine that cuts sheet metal by passing a blade through it.
2. (Physics) A deformation of an object in which parallel planes remain parallel
but are shifted in a direction parallel to themselves; "the shear changed
the quadrilateral into a parallelogram."
|
= |
|
* |
|
A generalized transform object represented internally
as a 4x4 double-precision floating point matrix. The mathematical representation
is row major, as in traditional matrix mathematics. A Transform3D is used to
perform translations, rotations, and scaling and shear effects.
A transform has an associated type, and all type classification is left to the
Transform3D object. A transform will typically have multiple types, unless it
is a general, unclassifiable matrix, in which case it won't be assigned a type.
The Transform3D type is internally computed when the transform object is constructed
and updated any time it is modified. A matrix will typically have multiple types.
For example, the type associated with an identity matrix is the result of ORing
all of the types, except for ZERO and NEGATIVE_DETERMINANT, together. There
are public methods available to get the ORed type of the transformation, the
sign of the determinant, and the least general matrix type. The matrix type
flags are defined as follows:* ZERO - zero matrix. All of the elements in the
matrix have the value 0.
* IDENTITY - identity matrix. A matrix with ones on its main diagonal and zeros
every where else.
* SCALE - the matrix is a uniform scale matrix - there are no rotational or
translation components.
* ORTHOGONAL - the four row vectors that make up an orthogonal matrix form a
basis, meaning that they are mutually orthogonal. The scale is unity and there
are no translation components.
* RIGID - the upper 3 X 3 of the matrix is orthogonal, and there is a translation
component-the scale is unity.
* CONGRUENT - this is an angle- and length-preserving matrix, meaning that it
can translate, rotate, and reflect about an axis, and scale by an amount that
is uniform in all directions. These operations preserve the distance between
any two points, and the angle between any two intersecting lines.
* AFFINE - an affine matrix can translate, rotate, reflect, scale anisotropically,
and shear. Lines remain straight, and parallel lines remain parallel, but the
angle between intersecting lines can change.A matrix is also classified by the
sign of its determinant:NEGATIVE_DETERMINANT - this matrix has a negative determinant.
An orthogonal matrix with a positive determinant is a rotation matrix. An orthogonal
matrix with a negative determinant is a reflection and rotation matrix.The Java
3D model for 4 X 4 transformations is:
[ m00 m01 m02 m03 ] [ x ] [ x' ] [ m10 m11 m12 m13 ] . [ y ] = [ y' ] [ m20 m21 m22 m23 ] [ z ] [ z' ] [ m30 m31 m32 m33 ] [ w ] [ w' ] x' = m00 . x+m01 . y+m02 . z+m03 . w y' = m10 . x+m11 . y+m12 . z+m13 . w z' = m20 . x+m21 . y+m22 . z+m23 . w w' = m30 . x+m31 . y+m32 . z+m33 . w
Note: When transforming a Point3f or a Point3d, the input w is set to 1. When
transforming a Vector3f or Vector3d, the input w is set to 0.
| Method |
|---|
| Transform3D( ) (Default : Identity) |
| Transform3D( Matrix4d mat ) |
| Transform3D( Matrix3d rot, Vector3d trans, double scale ) |
| Transform3D(..... see the doc API ) |
| void set( Matrix4d mat ) |
| void set( Matrix3d rot, Vector3d trans, double scale ) |
| public final void get(Matrix4d matrix) ..... VOID ! |
|
public final void mul(Transform3D t1) ..... this = this * t1 |
|
public final void mul(Transform3D t1, Transform3D t2) ..... this = t1*t2 |
| Setting the transform to identity | void setIdentity( ) |
|---|---|
| Setting the transform to a translation | void set( Vector3d trans ) |
| Setting the transform to a rotation | void rotX( double angle ) |
| ... rotY, rotZ | |
| only about angle passing through the origin | void set( AxisAngle4d axang ) |
| set( Matrix3d rot ) | |
| Setting the transform to a scale factor (uniform or XYZ) | void set( double scale ) |
| void setScale( Vector3d scale ) | |
Method
| void setTranslation( Vector3d trans ) |
| void setRotation( AxisAngle4d axang ) |
| void setRotation( Matrix3d rot ) |
| void setEuler( Vector3d rollPitchYaw ) |
| void setScale( double scale ) |
| AxisAngle4f(float x, float y, float z, float angle) |
Constructs and initializes a AxisAngle4f from the specified xyzw coordinates. |
| AxisAngle4f(Vector3f axis, float angle) |
Constructs and initializes an AxisAngle4f from the specified axis and angle. |
| Method |
|---|
| void transform( Point3d inout ) |
| void transform( Point3d in, Point3d out ) |
| void transform( Vector3d inout ) |
| void transform( Vector3d in, Vector3d out ) |
Shape3D shape = new Shape3D( geom, app );
. . .
Transform3D transLeft = new Transform3D( );
transLeft.set( new Vector3d( -1.0, 0.0, 0.0 ) );
. . .
TransformGroup group = new TransformGroup( );
group.setTransform( transLeft );
group.addChild( shape );
rotateAngle = Math.PI/10.0;
rotateXPlus = new Transform3D();
rotateXPlus.rotX(rotateAngle);
tmpT = new Transform3D(rotateXPlus);
viewTransform.mul(tmp, viewTransform)
System.out.println("Rotation Plus X ");
System.out.println(viewTransform);
viewTransformGroup.setTransform(viewTransform);